You’re an evolutionary organism with a finely tuned neural network, capable of absorbing data and adapting with these various instruments. Your eyes take in photons and your ears take in waveforms which ripple in the air.
With time and the iteration of science with respect to the death of the universe, asteroids, and galaxies set on a collision course, what are we to do?
The inevitable challenges facing humanity will force us to become machines or part of machines. Cyberpunk will be real. We had the industrial revolutions of Britain and America. Now comes the AI revolution.
Once AI begins to jailbreak physics, bioengineering integration will be mainstream. Interested to see what will happen at the nanoscale, like Mr Feynman said, “There’s plenty of room at the bottom”.
The list is infinite. The limit is physics, and that’s a big limit. Not to mention, once robots are everywhere, the economy also has a big limit. I really hope the stars of the show who are going all in, get it right.
Once the AI understands our sensors and effectors, the strings, pullies, functions and actuators that make us, us, then I think most of humanity will willingly adapt. It is the next phase in our evolution.
What does this mean for humanity, the human experience, well, whatever it means, and whatever happens, let’s not lose what makes humanity great.
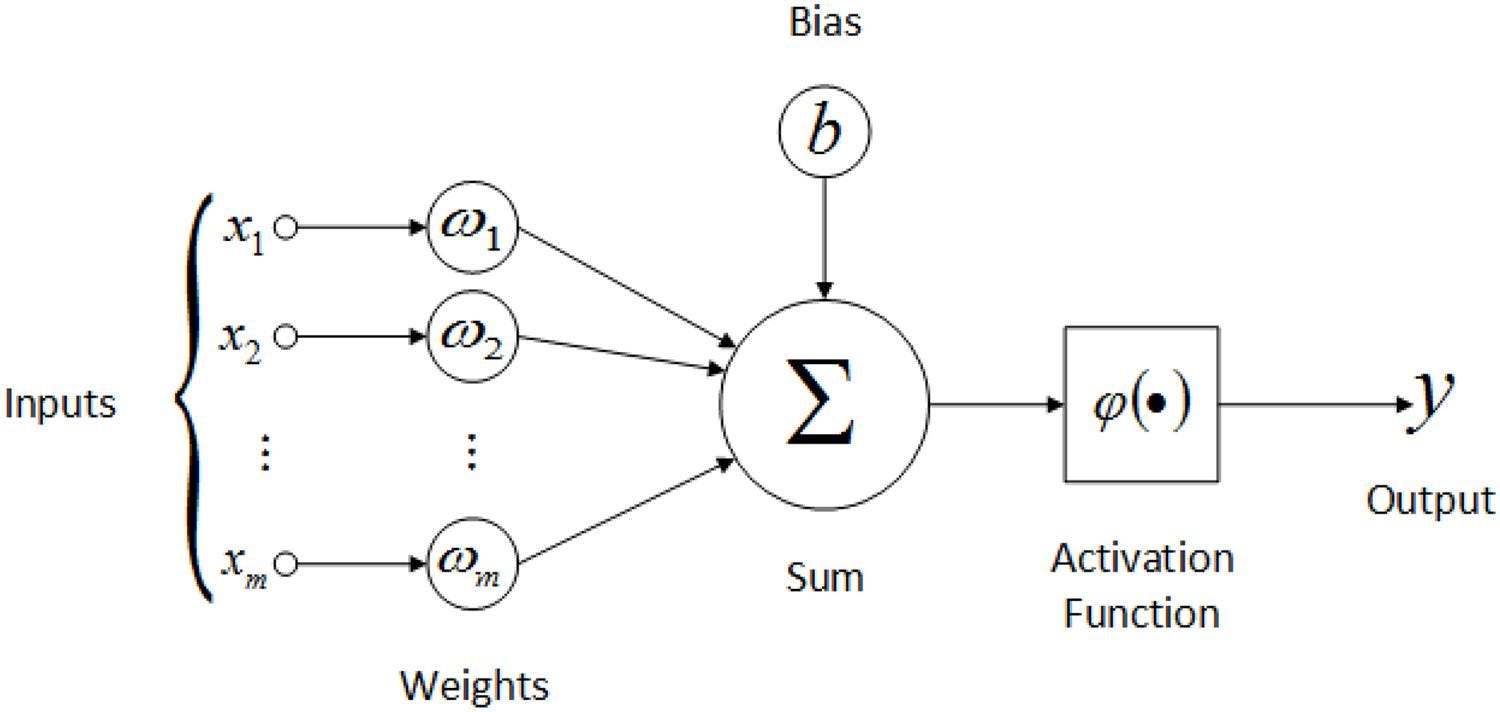
Mathematical Model of McCulloch-Pitts Neuron
- Input: Neurons take multiple inputs. Let’s call the inputs
where each
\[( x_i )\]is either 0 or 1 (binary).
- Weights: Each input has an associated weight. Let’s call the weights
which determine the importance of each input.
- Summing: Multiply each input
by its corresponding weight
\[( w_i )\]and then sum them all:
\[S = x_1w_1 + x_2w_2 + \dots + x_nw_n\]- Threshold: If the sum ( S ) is greater than or equal to a certain threshold value
the neuron fires (outputs 1). Otherwise, it doesn’t fire (outputs 0):
\[\text{Output} = \begin{cases} 1 & \text{if } S \geq \theta \\ 0 & \text{if } S < \theta \end{cases}\]Warren McCulloch said throughout his scientific career he always wanted to know “What is a number that a man may know it, and a man that he may know a number?”
“What is a number that a man may know it?” questions the fundamental nature of numbers and how humans are able to understand abstract concepts like numbers. This part relates to the philosophical and neurological mechanisms that allow human brains to grasp mathematical constructs.
“A man that he may know a number” emphasizes the reverse relationship, how humans, as biological entities with neurons and limited perceptual systems, manage to comprehend abstract concepts. It implies a question about the nature of human cognition itself and what makes humans capable of understanding abstract ideas like numbers, which are not directly observable or tangible in the natural world.
McCulloch delves into these questions through his work on neural networks and cognition. His mention of frogs and their visual systems: “what a frog’s eye tells the frog’s brain” refers to his study on how biological systems (like a frog’s visual processing) interpret sensory input, which parallels how human brains might process complex abstract information, like numbers.
“If I do it, there is a mechanism that can do it.”